引言
永磁同步电机由于效率高、结构简单、噪声小等显著优点,被应用在航天、航空、电动汽车等领域,因此永磁同步电机需要具有更高的安全性和可靠性。但在实际运行中,可能发生定子绕组匝间短路、永磁体失磁、转子偏心等故障,其中匝间短路故障发生最为频繁[1]。永磁同步电机由于环境潮湿、机械振动、瞬时过电压等原因可能导致绕组绝缘破损,造成电机匝间短路故障的发生,进一步影响电机温度场的分布。如不及时诊断故障,严重时将导致停机和人员伤亡,因此对永磁同步电机匝间短路故障温度场的研究是十分必要的[2]。
对于永磁同步电机匝间短路的研究,主要包括匝间短路故障的分析和诊断[3-6]。例如,通过建立匝间短路故障的数学模型,提出了一种价值函数,分析其中的直流和2次谐波分量来诊断故障[7]。在分析故障的三相等效电路时,如考虑饱和与空间谐波的影响,还能估计故障的严重度并对故障进行定 位[8]。为降低匝间短路故障对电机的影响,可以采用降低功率运行的方法减小短路故障电流,从而减小故障产生的热应力,增加电机的使用寿命[9]。
在电机温度场的研究中,由于永磁同步电机运行时,永磁体温度过高会使其部分失磁,影响电机的电磁性能,因此永磁同步电机温度场的精准计算是十分重要的。在电机温度场的计算方面,主要有两种方法:第一种方法为有限元法,通过建立有限元模型,计算出对应部分的热生成率,输入到模型中仿真,可以得到电机的温度分布[10]。通常情况下对于散线的绕组,需要考虑浸漆和绕组间空气隙的影响,建立等效绕组和等效绝缘来替代计算[11]。为减小计算的误差,部分学者分析转子部分[12]和端部绕组[13]损耗的影响。在电机运行时,温度改变会影响材料的导热性能,电磁场和温度场具有耦合关系。为了准确考虑耦合关系,建立了磁热耦合的有限元模型,对磁场和温度场结果进行迭代耦合计 算[14-16]。但影响温度场计算结果的因素有很多,其中冷却方式是研究温度场分布的关键,主要分为自然冷却、风冷、水冷、油冷。为了考虑风扇对电机散热的影响,将流体与有限元法相结合,修正了流体流动和温度场变化的耦合方程,减小了计算量,提高了温度场计算的精度[17-19]。第二种方法是建立集总参数热路模型,忽略物体内部的温度变化,计算出相应部件的热容和热阻,得到主要部件的平均温度。通过建立集总参数热路模型,能够准确预测出电机各个关键点的温度,并且与实验结果基本相同[20]。
在故障温度场的研究方面,文献[21]研究了感应电机匝间短路故障温度场,在不同位置和不同程度故障时,分析感应电机定子绕组和机壳部分温度的变化规律。如果利用温度传感器对电机的绕组进行在线监测,就可以准确地诊断出匝间短路故障的位置[22]。在研究故障温度场时,不仅能够分析匝间短路故障,还可以对感应电机转子导条断裂故障进行分析,提取故障特征量,进而研究故障产生的原因以及有效的诊断方法[23]。
国内外研究学者分别对永磁同步电机匝间短路故障的电磁场和诊断方法进行了详细研究,但对故障温度场的研究却很少,而且不够全面和深入。本文利用有限元方法对永磁同步电机匝间短路故障温度场进行了研究,以电机内电磁场为基础,分析了故障前后温度场的分布,为快速并准确地诊断永磁同步电机匝间短路故障提供依据。
1 有限元模型建立及实验测试
1.1 电机参数及有限元模型
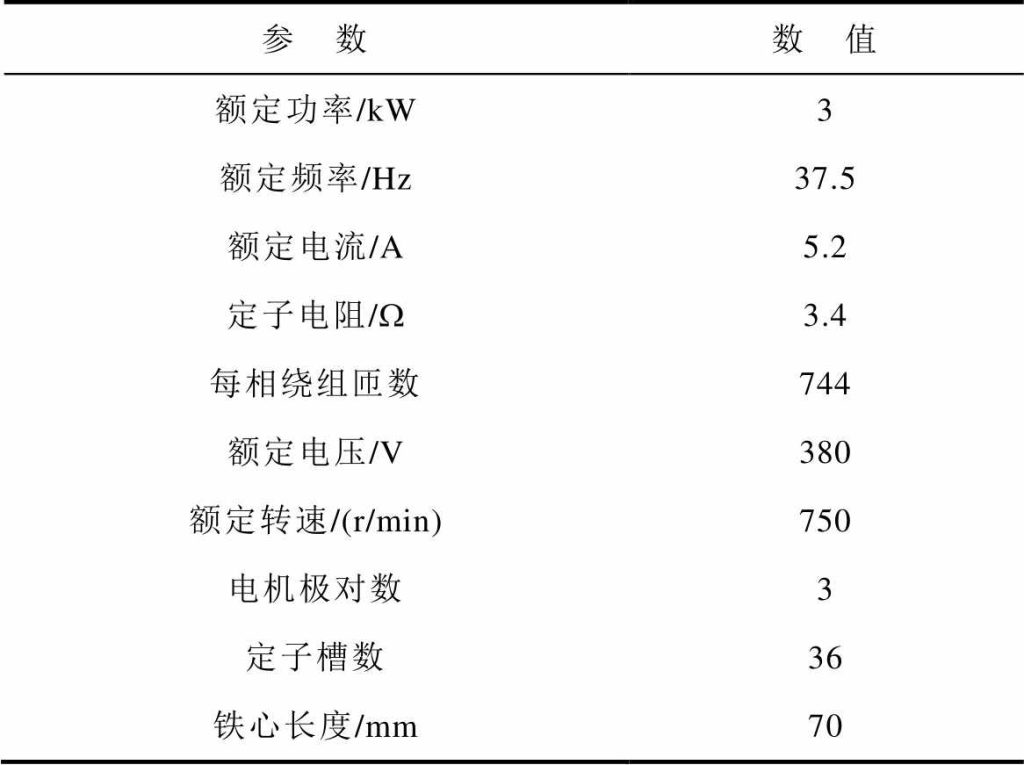
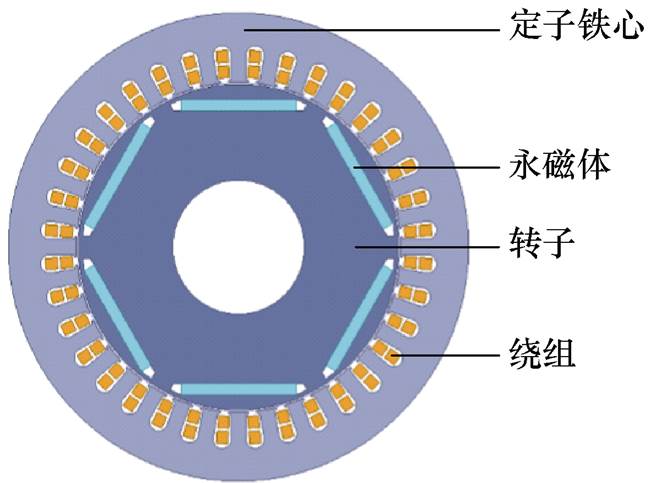
本文对一台永磁同步电机进行研究,电机基本参数见表1。通过电机基本参数建立了二维模型,如图1所示,仿真电机故障前的磁通密度分布如图2所示,可以看出磁通密度的分布具有对称性。
1.2 电机故障模型的建立
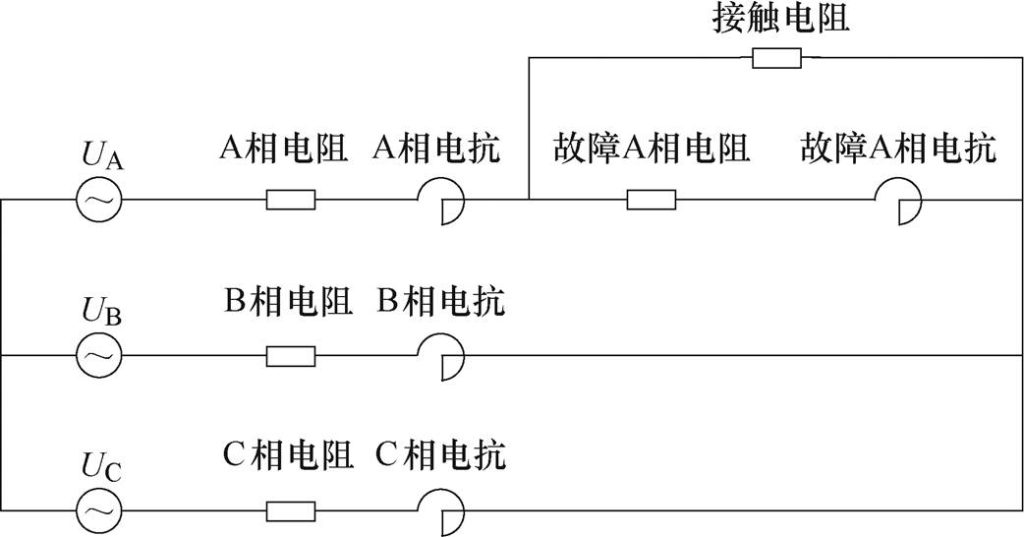
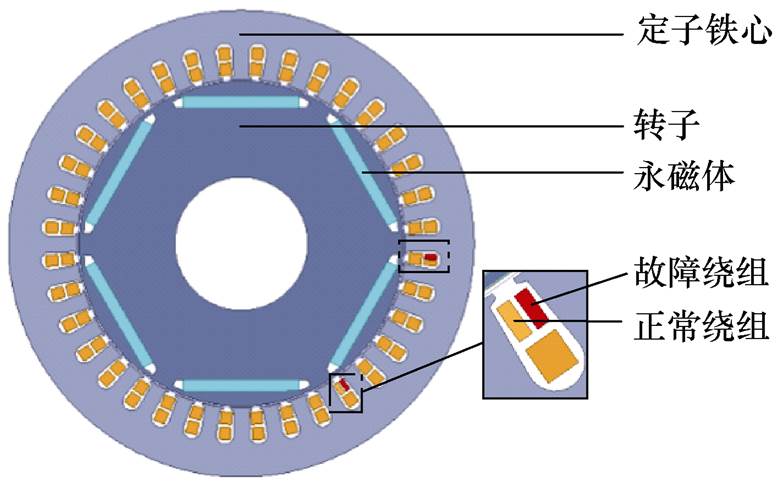
为了研究永磁同步电机匝间短路故障,本文假设A相为匝间短路故障相,则A相绕组被分为正常绕组部分和故障绕组部分,通过在故障绕组的两端并联接触电阻来模拟故障情况,电机匝间短路故障的等效电路如图3所示。
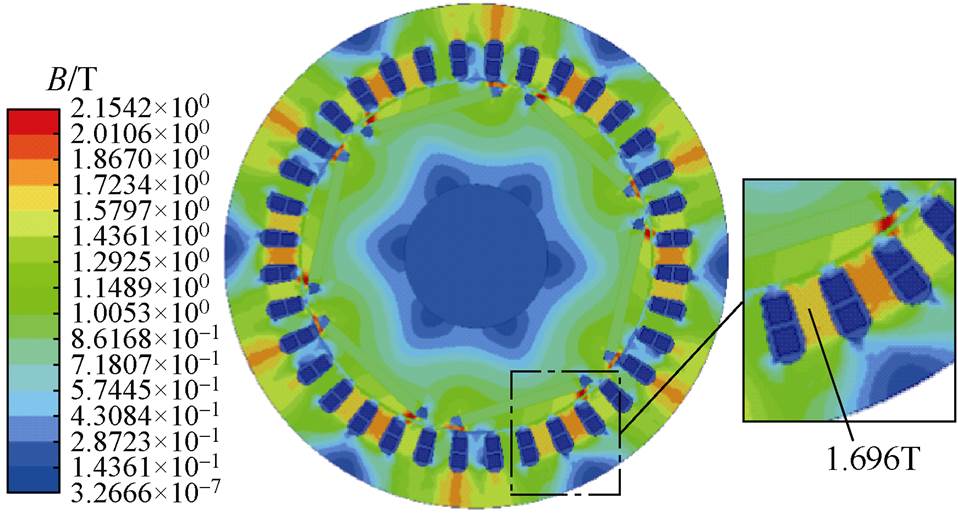
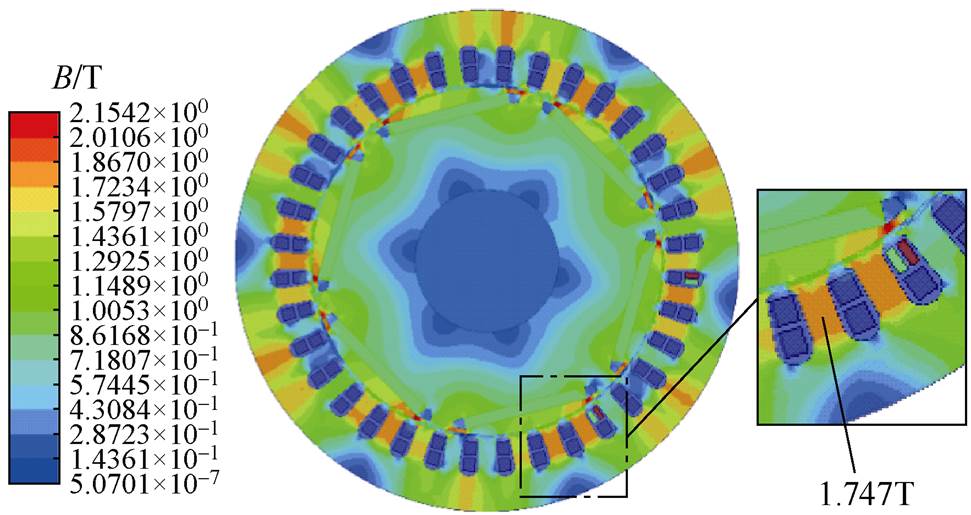
根据电机匝间短路故障的等效电路,建立了短路故障有限元模型如图4所示。发生匝间短路故障后,短路绕组中产生了环流,故障相电流增加,导致部分定子齿部磁通密度的饱和区增大,对电机局部损耗产生了影响,故障后电机的磁通密度分布如图5所示。
1.3 实验平台搭建
本文对一台永磁同步电机进行研究并搭建实验平台。为了进行匝间短路故障温度场的研究,对电机定子绕组部分重新下线,使电机能够在正常和不同程度匝间短路故障下进行实验,通过实验获取电机温度分布情况,并对温度数据进行分析,具体实验装置如图6所示。电机利用变频器起动,通过直流电源控制磁粉制动器的励磁电流,使电机在额定负载下工作。将滑动变阻器串联在短路支路,保护实验装置能够在安全的情况下运行,选择在阻值为1.2W时,进行31匝短路故障的实验。

为测量机壳表面风速和温度的数据,在电机机壳顶部处沿轴向设置了5个测量点A、B、C、D、E,A点靠近负载侧,E点靠近风扇侧。利用KANOMAX风速仪测量机壳顶部测量点的风速,Raynger ST30测温枪测量机壳顶部测量点的温度。在接线盒附近设置了不同程度的匝间短路接线柱,电机短路接线柱和机壳顶部测量点如图7所示。
研究永磁同步电机匝间短路故障温度场,需要获取实际运行时电机内各部分的瞬时温度。在电机内部埋设K型热电偶测定局部温度,利用TM902C测温计读取热电偶所测量的温度数据。在电机内部设置了6个测温点,测温点位置如图8所示。

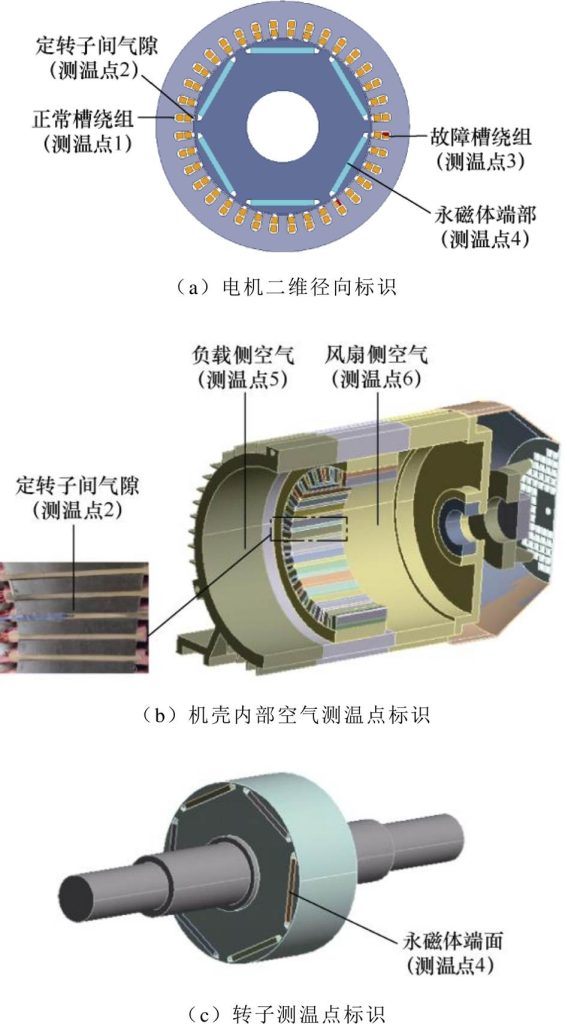
(1)在测量点1和测量点3处埋设热电偶来测量槽内绕组温度,测量点3在故障槽绕组处,为了比较故障前后电机内定子绕组温度的变化情况,在故障槽对侧的测温点1处,测量正常槽内绕组的温度。
(2)沿电机轴向方向,在定子铁心两侧的空气腔进行了测温,测温点5和测温点6分别测量了靠近负载侧和风扇侧的空气温度,具体位置如图8b所示。
(3)在电机接线盒对侧槽楔的测温点2处埋设热电偶,近似测量定转子间空气隙的温度。
(4)由于转子上的永磁体表面会产生涡流损耗,将热电偶埋设在测温点4处测量永磁体端面的温度,近似得到转子的温度数据,如图8c所示。
2 损耗计算和边界条件的施加
2.1 损耗计算
2.1.1 绕组铜耗
当电机三相绕组的电流和电阻分别相等时,绕组所消耗的铜耗等于其中某一相绕组铜耗的3倍。但匝间短路故障发生后,电机三相电流不平衡。如果故障相设置在A相,A相绕组的电阻被分为正常A相电阻和故障A相电阻,根据短路匝数计算故障绕组阻值,对应不同相绕组流过的电流大小分别计算损耗。故障相(A相)绕组的损耗计算公式为
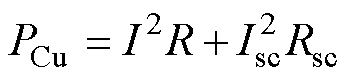 (1)
(1)式中,PCu为电机故障相绕组的铜耗;I为故障相正常绕组电流的有效值;R为故障相正常绕组的电阻;Isc为电机匝间短路故障绕组电流的有效值;Rsc为匝间短路故障绕组的电阻。
非故障相(B或C相)电流不相等,绕组的铜耗为
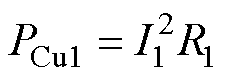 (2)
(2)式中,PCu1为电机非故障相绕组的铜耗;I1为电机非故障相绕组电流的有效值;R1为非故障相绕组 电阻。
2.1.2 定子铁心的基本铁耗
由于定子铁心是由硅钢片叠压而成,处于交变的磁场中会产生损耗,在定子铁心齿部和轭部的最大磁通密度不相等,为了准确地计算,将定子铁心分成两部分,定子齿部和轭部的铁心损耗如式(3)和式(4)所示[24]。
(1)定子齿部铁心的损耗为
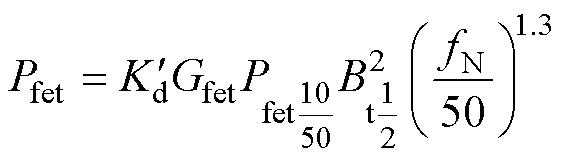 (3)
(3)(2)定子轭部铁心的损耗为
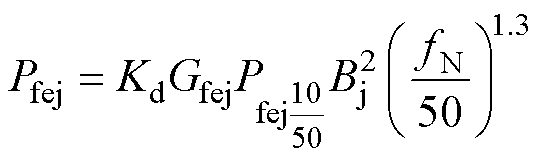
式中,Pfet和Pfej分别为定子齿部和轭部的铁心损耗;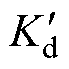
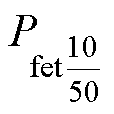
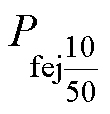
2.1.3 转子的涡流损耗
在永磁同步电机中,定子旋转磁场和转子的速度都为同步转速,通常忽略永磁体和转子的涡流损耗。本台电机的永磁体为稀土钕铁硼材料,电导率较高。在匝间短路故障时,电机磁路发生改变,永磁体的涡流损耗增加会导致温度明显升高,所以在电机温度场的计算中需要考虑涡流损耗的影响。由于实验电机通过变频器供电,气隙磁场含有较多时间和空间的谐波分量,解析法的计算比较困难,本文利用有限元法在永磁体上施加零电流源,分别计算了匝间短路故障前后永磁体的涡流损耗。
对永磁同步电机匝间短路故障前后电机各部分的损耗进行对比,见表2。在故障发生前后,定子齿部和定子轭部的铁心损耗变化较小;而永磁体涡流损耗增大了3倍,有必要在故障后考虑其对整体温度场的影响;三相绕组产生的损耗是最多的,为电机主要的发热部位,在故障后短路绕组的电流瞬间增大,在短时间内绕组产生的损耗迅速增加,使得电机其他部分的温度也随着上升。
表2 电机故障前后损耗对比

2.2 温度场模型建立
2.2.1 定子槽等效热模型
为了进行故障温度场的计算,建立模型时将槽内导体和绝缘分别建立,定子槽等效热模型如图9所示。根据电机的实际尺寸建立了三维温度场求解模型,为了方便对三维瞬态温度场的简化分析,做出下列假设:①等效绝缘和定子铁心紧密贴合; ②忽略定子槽内导线的温度差。
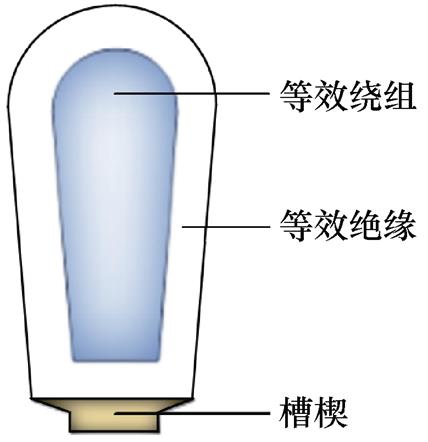
图9 定子槽等效热模型
Fig.9 Equivalent thermal model of the stator slots
根据槽内绝缘材料的参数,计算出等效绝缘的导热系数[25]为
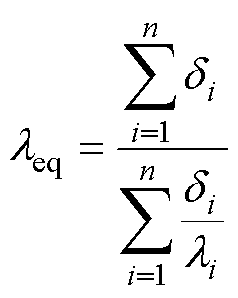 (5)
(5)式中,leq为等效绝缘的导热系数;di(i=1, 2, 3,…,n)为等效绝缘材料的宽度;li为绝缘材料平均导热 系数。
2.2.2 气隙的等效处理
由于样机采用全封闭结构,转子转动导致定转子间的空气流动,是定转子换热过程的关键。合理处理气隙的换热过程,将直接影响着电机内部温度计算的准确度。通过建立气隙实体并施加导热系数的方式来处理。其导热系数[25]为
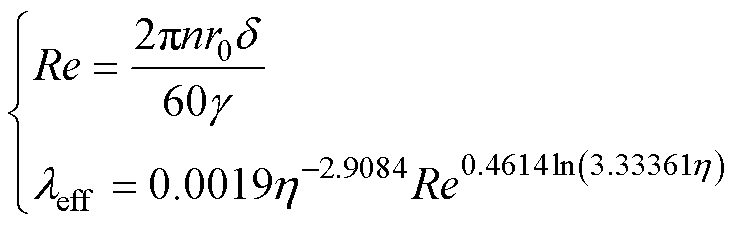
 (6)
(6)式中,Re为空气雷诺数;n为转子转速;r0为转子外径;d 为气隙长度;g 为空气运动粘度;leff为等效气隙的导热系数;h=r0/Ri为转子外径和定子内径的比值,其中,Ri为定子内径。
2.2.3 求解域边界条件
合理施加求解域的边界条件是准确仿真电机温度场分布的关键,具体求解域的边界如图10所示,其中,S1为机壳外表面,S2为机壳内表面和定子铁心外表面,S3为定子内表面和转子外表面,S4为转子铁心端面,S5为定子铁心端面。
计算对应位置的散热系数,S1为机壳的外表面,其表面散热系数与散热翅内的风速有关[21],有
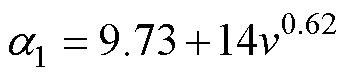 (7)
(7)式中,a1为机壳外表面散热系数;v为机壳表面的风速。
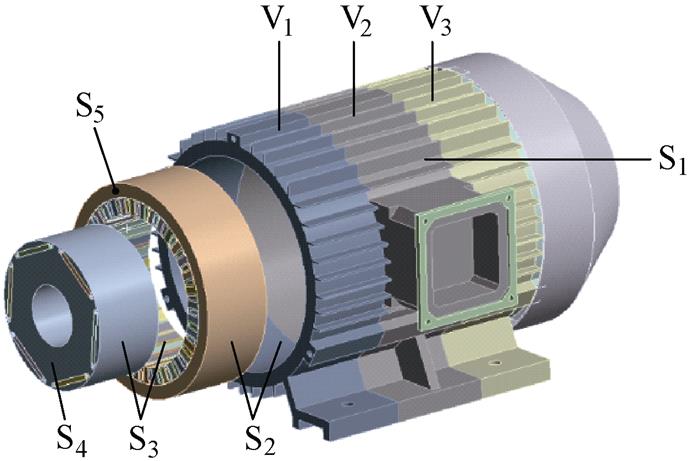
图10 求解域的边界
Fig.10 Boundaries of the solving region
电机冷却方式为封闭式自扇冷,风扇转动产生流动的空气,吹入机壳表面散热翅中冷却电机,散热翅中的风速从风扇侧到负载侧逐渐变小,为了准确考虑散热翅表面风速对电机机壳温度的影响,将有限元模型沿着轴向分割成V1、V2、V3三个部分。沿电机轴向位置的不同,机壳表面风速逐渐变化,所以对应不同的机壳部分,在外表面施加不同的散热系数。利用KANOMAX风速仪测量机壳表面各个位置的风速,把实验测量的风速数据按圆周方向取平均值。将数据分别代入到式(7)得V1、V2、V3三段模型表面的散热系数分别为22.10W/m2·℃、25.16W/m2·℃、28.97W/m2·℃。
S4为转子铁心端面,由于转子的转动带动机壳内部空气流动,使转子铁心端面散热效果增强,转子端面的散热系数[24]为
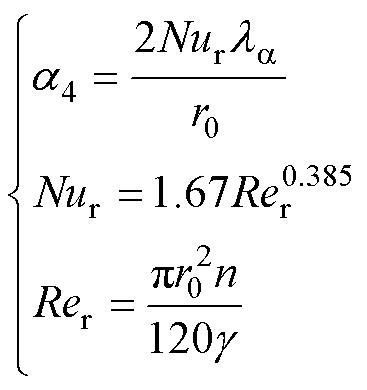 (8)
(8)式中,a4为转子端面散热系数;Nur为努塞尔系数;la 为空气的导热系数;Rer为转子端面空气的雷诺数。
S5为定子铁心端面,其散热系数[25]为
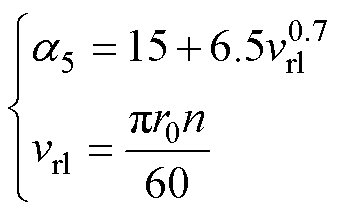
 (9)
(9)式中,a5为定子铁心端面散热系数;vrl为转子表面线速度。
2.2.4 机壳与铁心间接触热阻
机壳和定子铁心之间由于装配的影响,不是紧密贴合,中间存在较小的装配气隙层。由于空气的导热系数与固体相比较低,阻碍了热量从定子铁心到机壳的热传导,需要考虑其对电机温度场的影响,定子铁心与机壳接触部分的等效热阻[23]为

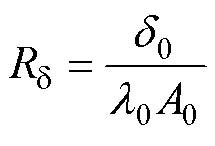 (10)
(10)式中,Rd 为定子铁心和机壳的接触热阻;d0为机壳和定子铁心间的气隙长度;A0为定子铁心和机壳间的导热面积;l0为静止薄空气层的导热系数。
3 电机故障前后温度场结果分析
3.1 三维瞬态温度场仿真结果分析
环境初始温度设置为20℃,当电机在正常情况下以额定负载运行至120min时,仿真出电机整体温度场云图,如图11所示。在正常情况下,由于电机三相电流基本一致,三相绕组产生热量相同,但电机接线盒部分散热效果较差,导致靠近接线盒部分定转子铁心温度略高于相邻部分。当电机A相绕组发生31匝短路时,故障绕组的电流迅速增大,导致电机三相绕组电流发生严重的不平衡,A相短路绕组电流增大,在局部出现过热的情况,导致电机整体温度的分布情况改变,温度云图如图12所示。
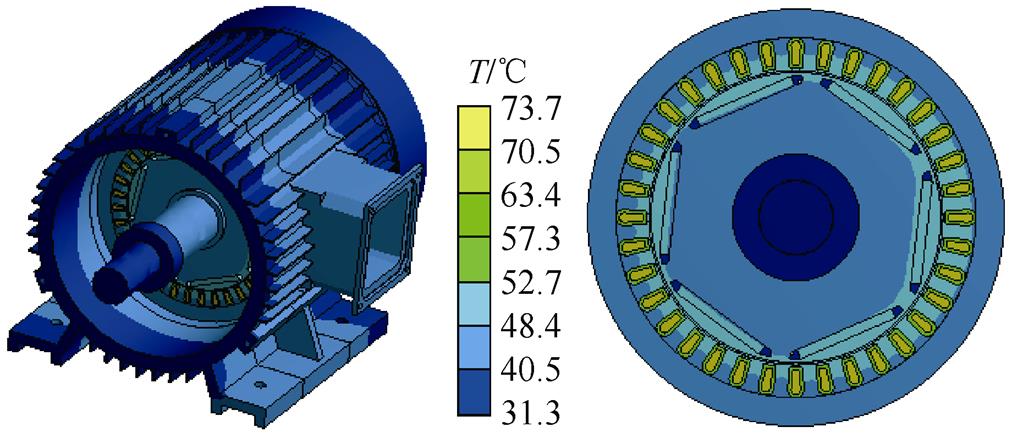
图11 故障前电机温度分布
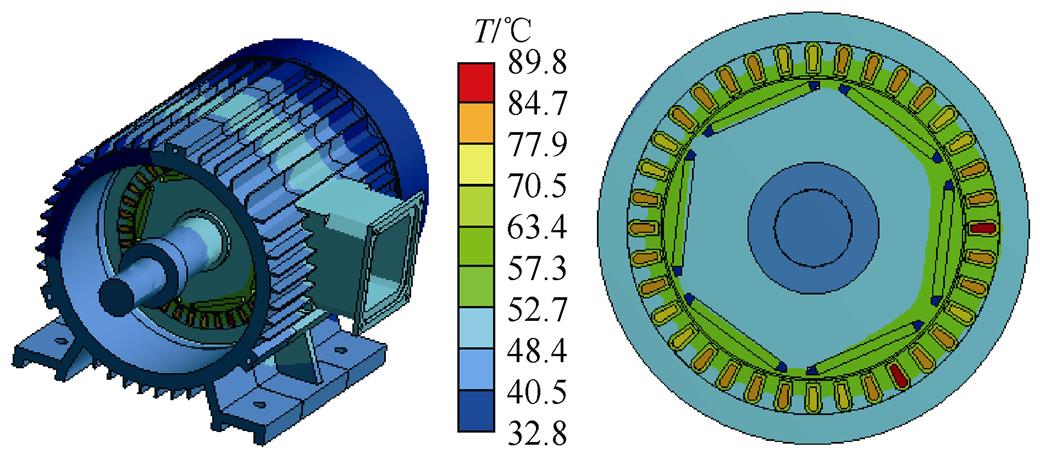
图12 匝间短路故障电机温度分布
3.2 故障前温度场实验和仿真结果分析
实验的样机为连续运行工作制,利用搭建的实验平台进行了故障前温度场实验,直到电机各部分温度达到稳态。
3.2.1 故障前温度场实验结果
1)机壳顶部风速和温度的关系
在实验平台进行额定负载实验,电机顶部有5个测量点分别为A、B、C、D、E,如图7所示。利用风速仪测量散热翅中的风速,红外测温仪测量出机壳顶部测温点的温度。运行至稳态后顶部5个点的温度和风速关系如图13所示。
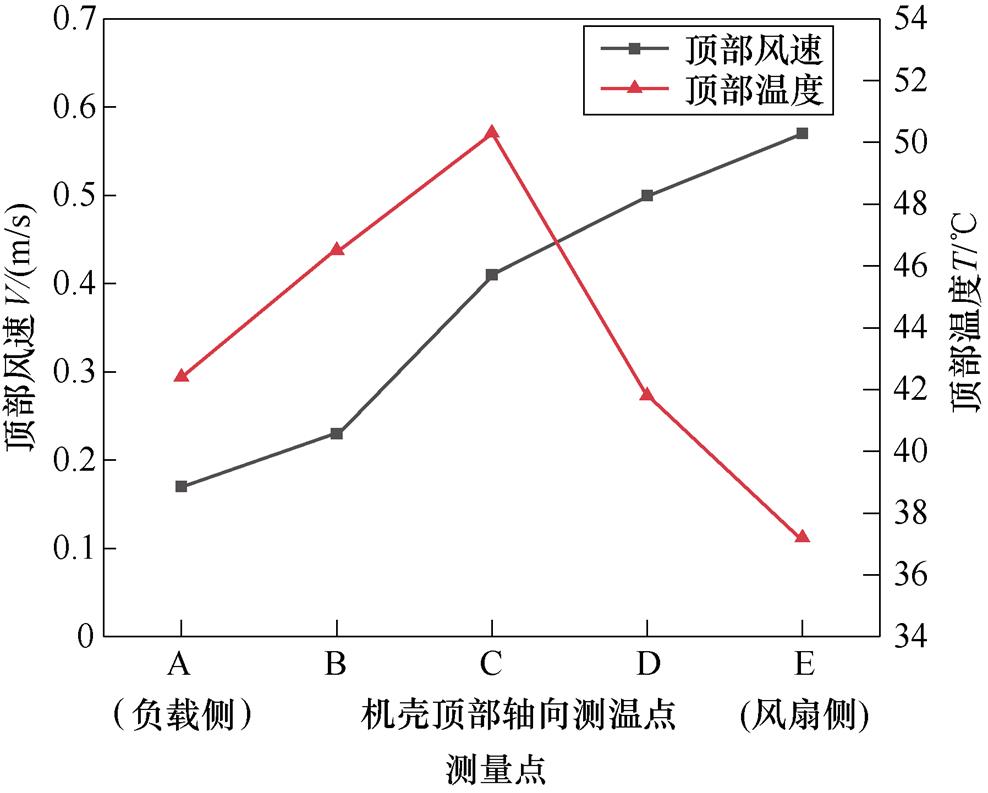
图13 实验测量点温度与风速的关系
Fig.13 The relation between temperature and wind speed at the experimental test points
由于电机采用封闭式自扇冷,沿着电机的轴向,从风扇侧到负载侧,散热翅表面的风速随着距离的增加而降低,散热效果也降低,使得靠近负载侧机壳的温度始终高于风扇侧机壳。电机内部的热量主要以热传导的方式从定子铁心传递到机壳,并且定子铁心处于机壳的中心位置,所以机壳的中心C点温度最高,沿轴向从负载侧到风扇侧,在机壳顶部呈现出先升高后降低的趋势。
2)电机内部空气温度对比
风扇的散热不仅影响着机壳表面散热翅的温度,对电机内部空气腔的温度也有所影响。在实验中对3个点的空气进行了测温,分别是电机内负载侧的空气腔、风扇侧的空气腔和定转子间空气隙,将3个测温点空气温度的实验值进行对比,如图14所示。
由于转子的转动带动着内部空气的流动,与负载侧和风扇侧的空气相比,定转子间空气的流动速度较大,散热效果较好,所以在电机运行初期,定转子间空气的温度低于两侧空气腔的温度。待电机温升达到稳态后,定转子间空气隙温度和风扇侧空气几乎保持一致。从图14中可以看出,由于风扇散热的影响,在电机内部负载侧空气温度恒大于风扇侧,将导致两端空气的导热系数不同,使得电机负载侧和风扇侧的端部绕组、定转子铁心端部等部分散热效果不同。
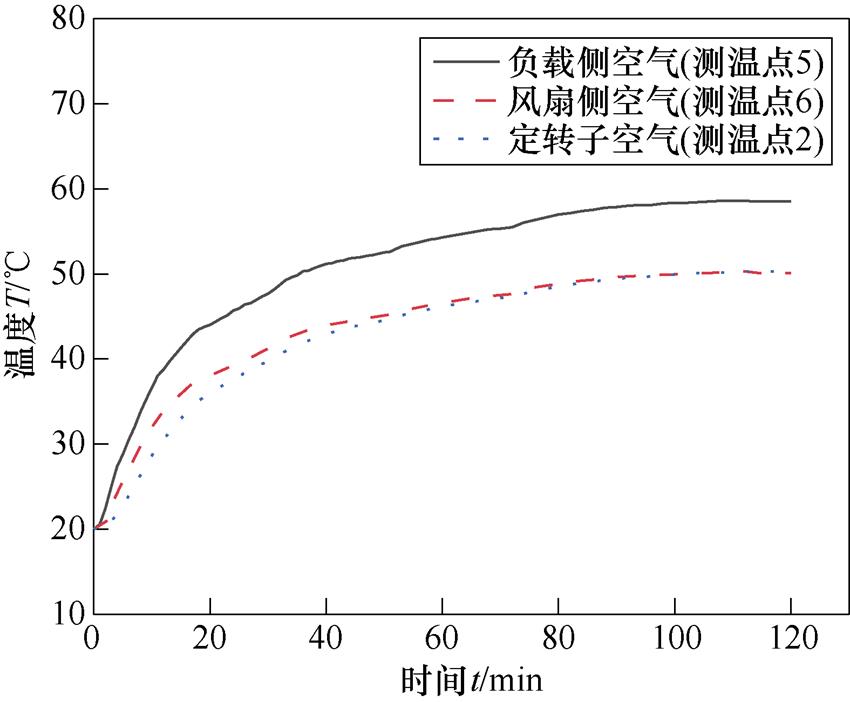
图14 电机内部空气温度的实验值
Fig.14 Experimental values of air temperature inside the motor
3.2.2 故障前仿真和实验数据对比
在电机正常情况下,将对侧绕组(测温点1)和转子永磁体端面(测温点4)温度场的实验值和仿真值进行对比,如图15所示。
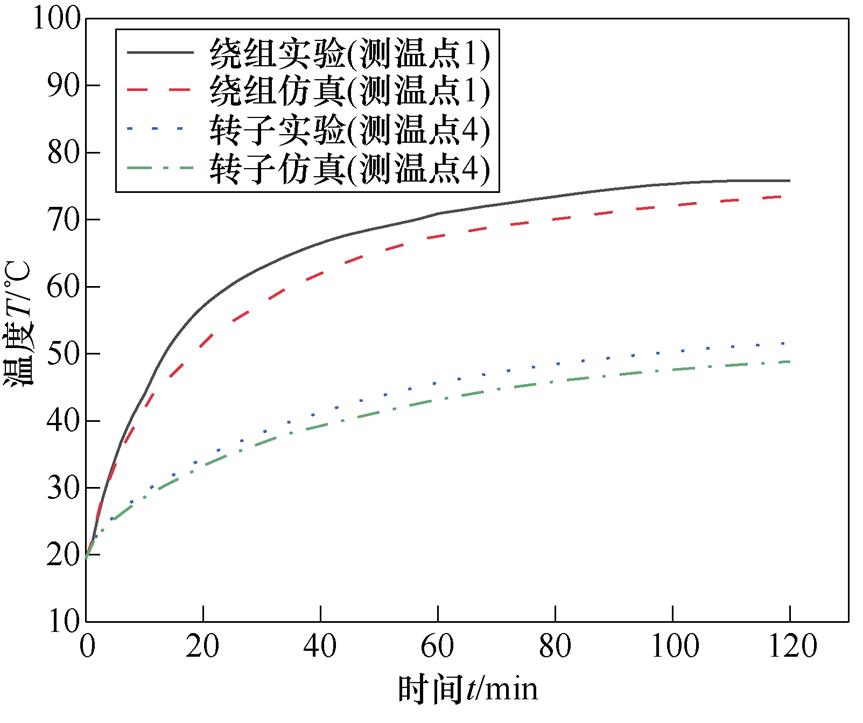
图15 绕组与转子温度的实验值和仿真值对比
Fig.15 Comparison of experimental values and simulation values of the winding and rotor temperature
可以观察出,对侧绕组和转子数据的仿真值恒低于实验值,但温度的基本趋势相同,误差都在 3℃内。产生误差的原因为:在使用式(5)计算等效绝缘的导热系数时,假设在浸漆完全的情况下,计算出等效绝缘的导热系数偏高,会导致温度场的仿真值低于实验值。
定子绕组和转子温度差较大,样机的定子绕组由于铜耗产生热量,主要通过机壳散热;而转子部分产生损耗较小,其热量主要由定子绕组产生并通过空气传递,为转子温度升高的主要因素。
3.3 故障后温度场实验和仿真结果分析
利用搭建的实验平台进行匝间短路故障温度场实验,直到电机各部分温度达到稳态。由于在实际短路时环流可以达到额定电流的10倍左右。为了保证实验设备的安全,并进行电机匝间短路故障温度场数据的测量与分析,在进行31匝短路故障实验时,短路支路中串联1.2W 的电阻。
3.3.1 故障后温度场实验结果
在永磁同步电机发生31匝短路故障时,根据温度场实验值绘制的曲线如图16所示。
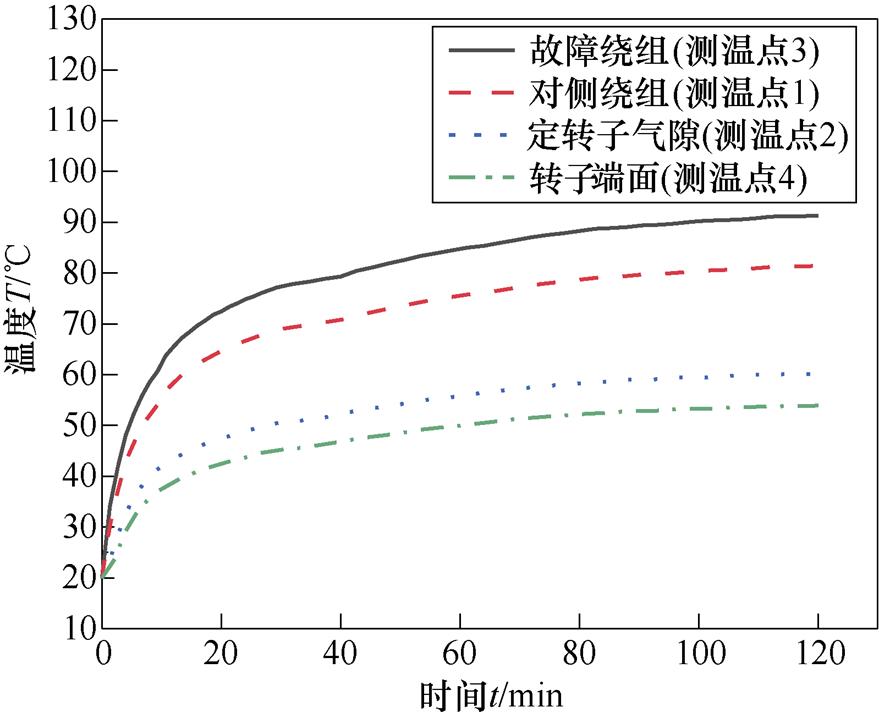
图16 电机故障后关键位置点的温度场实验值
在匝间短路故障发生后,由于故障绕组电流迅速增大,产生热量较多,故障点的短路绕组是电机温度最高的部分,与对侧的绕组相比,温度高于对侧绕组约10℃;而定转子间空气隙的温度介于定子和转子之间,更接近于转子温度;由于转子产生热量较小,所以转子的温度是最低的。
3.3.2 故障后仿真和实验数据对比
利用有限元方法仿真出电机关键部件的瞬态温度曲线,电机故障后关键位置点的温度场仿真值如图17所示。
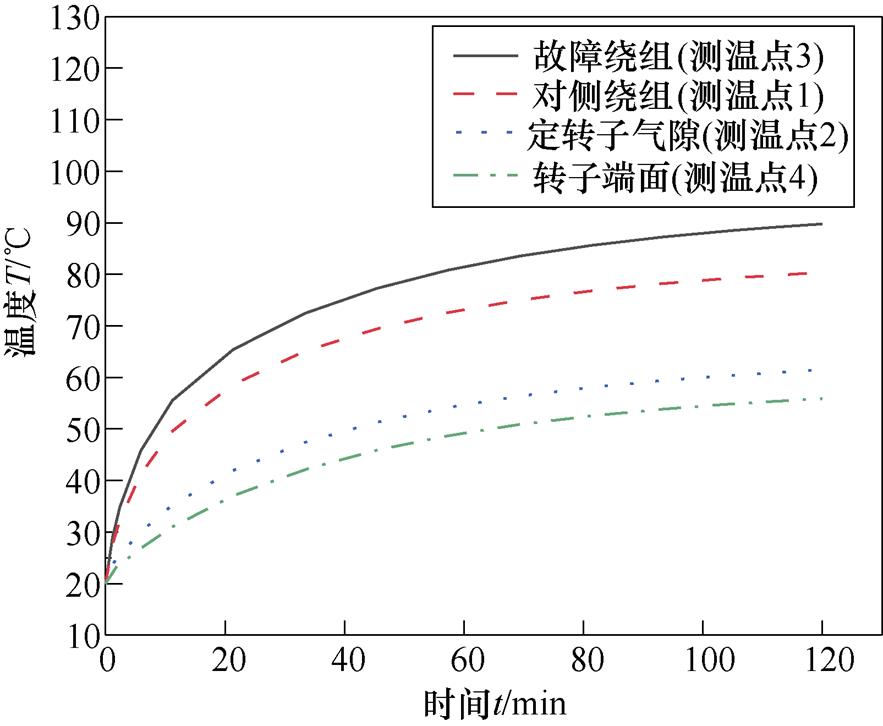
图17 电机故障后关键位置点的温度场仿真值
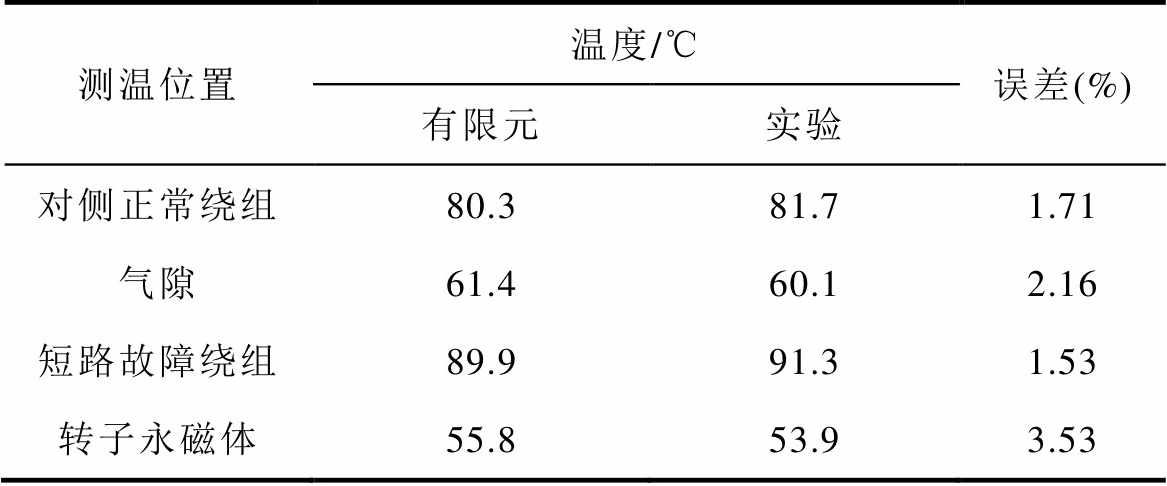
对比图16和图17中短路情况下温度场的仿真值和实验值数据,比较结果见表3。有限元仿真结果和实验值的误差在允许的范围之内,证明电机温度场仿真结果能准确地反映电机实际温度。
表3 故障后温度场的仿真值和实验值比较
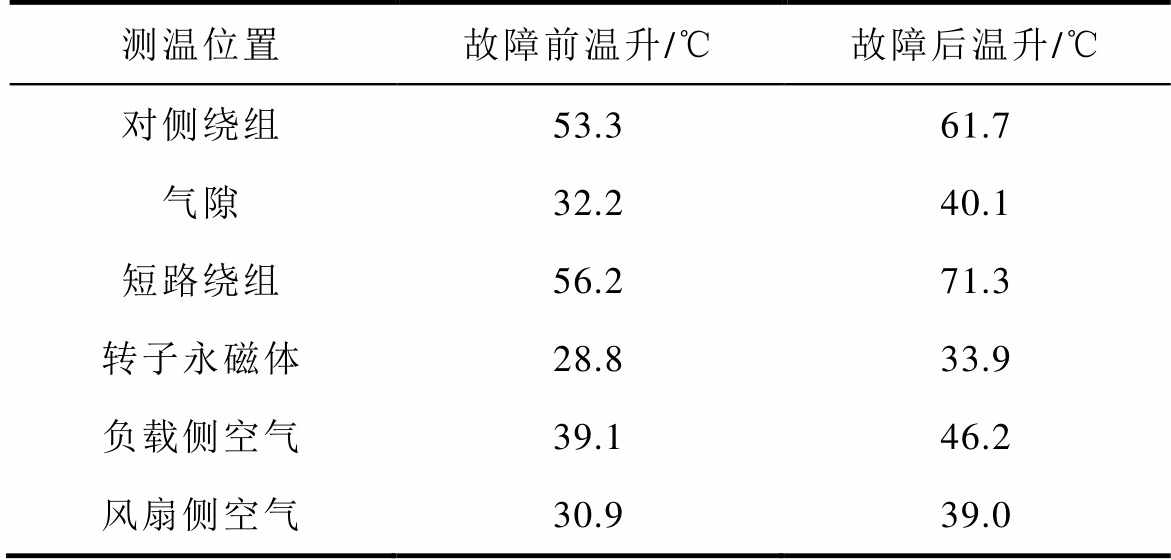
根据所测量的实验数据,对比匝间短路故障前后关键位置点温升的测量值,见表4。通过观察实验数据可以得出温度场变化的规律:在永磁同步电机匝间短路故障发生后,由于故障绕组部分的电流瞬间增大,产生了较多的热量,与故障前相比,故障绕组温度升高了15℃,是温升差别最大的部位,而对侧正常绕组在故障后温度升高了8℃;对于转子部分,由于定子绕组的热量是通过空气传递到转子部位的,空气的导热系数较小,所以转子部分的温升仅为5.1℃;介于定转子间的气隙,温度介于定子绕组与转子之间,在匝间短路故障后,定转子间气隙与转子的温度差变大;对于空气腔的温度,在短路故障发生后,随着定子绕组的温度升高,引起了负载侧和风扇侧空气腔的温度也逐渐升高。电机运行至稳态时,故障绕组中的热量通过定子铁心和空气传递到其他的部位,使得电机的整体温度明显升高并处于平衡状态。
表4 故障前后关键位置点温升测量值对比
4 结论
本文以一台永磁同步电机为例,采用有限元法,研究了负载情况下电机正常运行和匝间短路故障时的温度场,并通过实验进行了验证,分析了故障前后电机温度分布。得出以下结论:
1)考虑了永磁体涡流损耗、电机散热翅处空气流动和电机负载侧与风扇侧气隙端腔空气温度对电机温度场的影响,把故障前后仿真的温度场数据与实验测量数据进行对比分析,得到的结果基本一致,误差在允许的范围之内。由此可见,能够通过仿真结果准确地反映电机实际的温度分布及故障前后温度的变化情况。
2)在永磁同步电机发生匝间短路故障时,电机故障槽绕组的局部温度会瞬间升高,并且大于对侧正常绕组的温度。绕组温度过高会导致绝缘加速老化,如果不及时处理将会发展为更为严重的相间短路故障,甚至损坏电机。
3)由于风扇散热的影响,电机内部负载侧端腔和风扇侧端腔空气温度不相等,负载侧端腔的空气温度高于风扇侧,这会导致两侧的散热效果不同。随着匝间短路故障的发生,两侧端腔的空气温度也随着电机整体温度的升高而升高。
4)正常运行时定转子间气隙的温度高于转子部分,在31匝匝间短路故障后,定转子间气隙和转子的温度随着故障绕组温度的升高而增大,并且在故障发生后,两者的温度差也逐渐变大。
5)匝间短路故障会使得故障绕组温度迅速升高,因此可以通过实时监测电机关键元件的温度,在故障的早期及时发现异常情况,为匝间短路故障的诊断提供依据。
参考文献
[1] Zafarani M, Bostanci E, Yuan Qi, et al. Inter-turn short circuit faults in permanent magnet synchronous machines: an extended review and comprehensive analysis[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 2173-7191.
[2] 魏永田, 孟大伟, 温嘉斌. 电机内热交换[M]. 北京:机械工业出版社, 1998.
[3] 陈柄任, 李颖晖, 李哲, 等. 基于流形学习的PMSM早期匝间短路故障特征量提取[J]. 电力系统保护与控制, 2016, 44(17): 18-24.
Chen Bingren, Li Yinghui, Li Zhe, et al. Feature extraction of inchoate interturn short circuit fault for PMSM based on manifold learning[J]. Power System Protection and Control, 2016, 44(17): 18-24.
[4] 潘超, 米俭, 王格万, 等. 基于场路耦合的变压器绕组匝间短路电磁谐响应分析方法[J]. 电工技术学报, 2019, 34(4): 673-682.
Pan Chao, Mi Jian, Wang Gewan, et al. Electro- magnetic harmonic response analysis method of inter- turn short circuit in transformer winding based on field circuit coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 673-682.
[5] 张艳辉, 郑晓钦, 吴新振, 等. 基于有限元场路耦合的十二相整流发电机系统定子匝间短路分析[J]. 电工技术学报, 2019, 34(9): 1842-1849.
Zhang Yanhui, Zheng Xiaoqin, Wu Xinzhen, et al. Analysis of stator winding inter-turn short circuit on a 12-phase rectifier generator system based on finite element field-circuit coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1842-1849.
[6] 李垣江, 张周磊, 李梦含, 等. 采用深度学习的永磁同步电机匝间短路故障诊断方法[J]. 电机与控制学报, 2020, 24(9): 173-180.
Li Yuanjiang, Zhang Zhoulei, Li Menghan, et al. Fault diagnosis of inter-turn short circuit of per- manent magnet synchronous motor based on deep learning[J]. Electric Machines and Control, 2020, 24(9): 173-180.
[7] 丁石川, 王清明, 杭俊, 等. 计及模型预测控制的永磁同步电机匝间短路故障诊断[J]. 中国电机工程学报, 2019, 39(12): 3697-3708.
Ding Shichuan, Wang Qingming, Hang Jun, et al. Inter- turn fault diagnosis of permanent magnet synchronous machine considering model predictive control[J]. Proceedings of the CSEE, 2019, 39(12): 3697-3708.
[8] Yuan Qi, Bostanci E, Zafarani M, et al. Severity estimation of interturn short circuit fault for PMSM[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7260-7269.
[9] Cintron-Rivera J, Foste S, Strangas E. Mitigation of turn-to-turn faults in fault tolerant permanent magnet synchronous motors[J]. IEEE Transactions on Energy Conversion, 2015, 30(2): 465-475.
[10] Wang Ning, Wang Huifang, Yang Shiyou. 3D eddy current and temperature field analysis of large hydro-generators in leading phase operations[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 210-215.
[11] Huang Xuzhen, Tan Qiang, Li Liyi, et al. Winding temperature field model considering void ratio and temperature rise of a permanent-magnet synchronous motor with high current density[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2168-2177.
[12] Zhao Nannan, Zhu Ziqiang, Liu Weiguo. Rotor eddy current loss calculation and thermal analysis of permanent magnet motor and generator[J]. IEEE Transactions on Magnetics, 2011, 47(10): 4199-4202.
[13] Wrobel R, Mlot A, Mellor P. Contribution of end- winding proximity losses to temperature variation in electromagnetic devices[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 848-857.
[14] Si Jikai, Zhao Suzhen, Feng Haichao, et al. Analysis of temperature field for a surface-mounted and interior permanent magnet synchronous motor adopting magnetic-thermal coupling method[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 166-174.
[15] 郑迪, 王大志, 于林鑫, 等. 盘式永磁涡流驱动器的电磁-温度耦合解析模型[J]. 电工技术学报, 2019, 34(11): 2315-2323.
Zheng Di, Wang Dazhi, Yu Linxin, et al. Electro- magnetic-thermal analytical model of axial-flux per- manent magnet eddy current driver[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2315-2323.
[16] 韩雪岩, 宋聪. 基于磁热耦合法车用永磁同步电机温升计算及影响因素的研究[J]. 电机与控制学报, 2020, 24(2): 28-35.
Han Xueyan, Song Cong. Research on temperature rise influencing factors and calculation of permanent magnet synchronous motor for vehicle based on magneto-thermal coupling method[J]. Electric Machines and Control, 2020, 24(2): 28-35.
[17] Zhang Yujiao, Ruan Jiangjun, Huang Tao, et al. Calculation of temperature rise in air-cooled indu- ction motors through 3-D coupled electromagnetic fluid-dynamical and thermal finite-element analysis[J]. IEEE Transactions on Magnetics, 2012, 48(2): 1047-1050.
[18] 吴柏禧, 万珍平, 张昆, 等. 考虑温度场和流场的永磁同步电机折返型冷却水道设计[J]. 电工技术学报, 2019, 34(11): 2306-2314.
Wu Baixi, Wan Zhenping, Zhang Kun, et al. Design of reentrant cooling channel in permanent magnet synchronous motor considering temperature field and flow field[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2306-2314.
[19] 朱高嘉, 刘晓明, 李龙女, 等. 永磁风力发电机风冷结构设计与分析[J]. 电工技术学报, 2019, 34(5): 946-953.
Zhu Gaojia, Liu Xiaoming, Li Longnü, et al. Design and analysis of the ventilation structure for a per- manent magnet wind generator[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 946-953.
[20] EL-Refaie A, Harris N, Jahns T, et al. Thermal analysis of multibarrier interior PM synchronous machine using lumped parameter model[J]. IEEE Transa- ctions on Energy Conversion, 2004, 19(2): 303-309.
[21] 王艳武, 杨立, 孙丰瑞. 异步电动机定子绕组匝间短路三维温度场计算与分析[J]. 中国电机工程学报, 2009, 29(24): 84-90.
Wang Yanwu, Yang Li, Sun Fengrui. Simulation and analysis of 3D temperature field for stator winding short-circuit in asynchronous motor[J]. Proceedings of the CSEE, 2009, 29(24): 84-90.
[22] Mohammed A, Melecio J, Djurović S. Stator winding fault thermal signature monitoring and analysis by In Situ FBG sensors[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 8082-8092.
[23] Xie Ying, Wang Yunyang. 3D temperature field analysis of the induction motors with broken bar fault[J]. Applied Thermal Engineering, 2014, 66(1-2): 25-34.
[24] 谢颖, 辜承林. 笼型感应电动机三维全域温度场计算[J]. 中国电机工程学报, 2012, 32(36): 96-101.
Xie Ying, Gu Chenglin. Calculation of 3D whole domain thermal fields of squirrel-cage induction motors[J]. Proceedings of the CSEE, 2012, 32(36): 96-101.
[25] 鲍里先科А И, 丹科В Г, 亚科夫列夫А И. 电机中的空气动力学与热传递[M]. 魏书慈, 邱建甫, 译. 北京: 机械工业出版社, 1985.






